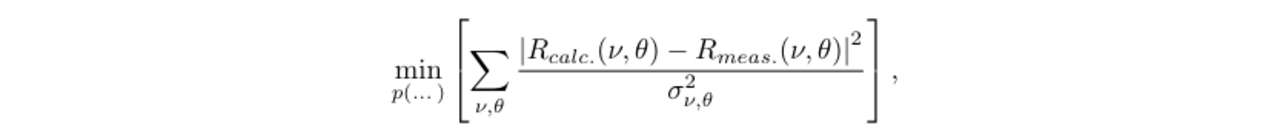
Optimization Method
A typical EUV reflectance data set consists of around 45 angles of incidence between near normal and close to 90◦at every given photon energy. In a stack of four layers on a substrate and assuming that the substrate’s optical constants are known, there are 4 ×2 optical constants, 5 roughness parameters and 4 thickness parameters, totaling to 17 unknowns. In the chosen model, the roughness parameters are independent of the wavelength, therefore there are 8 unique parameters (4 ×δ and 4 ×β) at each photon energy, and further 9 parameters (5 ×s, 4 ×h) for the global data set across the entire spectrum. At 80 measured photon energies, this means that 649 parameters must be determined on a basis of 3600 data points. The optimization problem is defined as follows:
Although the optimization problem in the equation could be solved directly, it is more efficient to break it down into two smaller optimization problems. For a fixed set of layer thicknesses and interfacial roughnesses as ’outer’ parameters, the optical constants as ’inner’ parameters of the optimization problem can be determined individually for all photon energies using a Levenberg-Marquandt algorithm. Thus, we run a global optimization algorithm to determine the 9 ’outer’ parameters and minimize the optical constants independently for every measured energy. Starting values for the optimizer are chosen from prior knowledge of the sample fabrication for s and h, while tabulated data is used for the optical constants. On a modern desktop computer, this can be solved within reasonable calculation time, using state-of-the-art optimization toolboxes (SciPy).
